T5.3 Cryptographie⚓︎

1. Chiffrement symétrique⚓︎

Brève historique de la cryptographie

La cryptographie est la discipline qui consiste à chiffrer et déchiffrer des messages afin de les protéger en les rendant secrets. La cryptanalyse est la discpline qui analyse les messages chiffrés (appelés aussi cryptogrammes) afin de les déchiffrer.

On trouve des utilisations de cryptographie depuis l'antiquité, comme par exemple l'utilisation d'une scytale ou encore le célèbre chiffre de César vu en classe de première qui consiste à effectuer un décalage des lettres du message, d'un nombre de lettres fixé à l'avance qui constitue la clé du système.

Bien d'autres procédés ont été inventés par la suite (lire à ce sujet l'excellent Histoire des codes secrets, de Simon Singh, Le Livre de Poche, disponible à la médiathèque du lycée) à des fins bien souvent militaires qui nécessitaient une grande confidentialité...

En 1586 Blaise de Vigènere met au pont un chiffrement polyalphabétique qui résistera près de 3 siècles. Le principe est de choisir une clé (par exemple NSI) et d'utiliser successivement un chiffre de César avec N pour la première lettre, puis un chiffre de César avec S pour la deuxième lettre, puis avec I pour la troisième, puis avec N pour la quatrième, puis avec S pour la cinquième, etc.

Au XX-ème siècle, l'avènement de l'ordinateur et de sa puissance de calcul a motivé de nombreuses recherches et découvertes dans le domaine de la cryptographie pour réussir à sécuriser non seulement les secrets militaires, mais également les transactions bancaires et plus généralement l'échange de nos données personnelles sur le web...

Principe d'un chiffrement

Un chiffrement est la transformation - à l'aide d'un algorithme - d'un texte clair en un texte incompréhensible, dit chiffré, à l'aide d'une clé de chiffrement.

L'algorithme est la plupart du temps connu, et la sécurité du chiffrement doit résider dans le secret de la clé ( Principe de Kerckhoffs).

Cette clé peut être la même pour chiffrer et déchiffrer: on parle alors de chiffrement symétrique. Si la clé de chiffrement et la clé de déchiffrement sont différentes, on parle de chiffrement asymétrique.

En pratique la clé est un nombre ou une fonction mathématique. Mais c'est parfois un texte ou une image...

Exercice 1: chiffre de César

ÉnoncéCorrection

Combien de clés différentes existe-t-il pour le chiffre de César?

Compléter le code suivant (utiliser les fonctions ord et chr pour la fonction decale :

def decale(lettre:str, cle:int) -> str:
    '''
    Décale une lettre majuscule de cle rangs dans l'alphabet.
    '''
    rang = ...(lettre) - ...(...)
    rang = (rang + ...) % ...
    return ...(rang)


def chiffre_cesar(phrase:str, cle:int) -> str:
    '''
    Chiffre le texte phrase avec la clé cle et renvoie le texte chiffré
    '''
    texte_chiffre = ""
    for ... in ...:
        texte_chiffre += ...
    return texte_chiffre

Déchiffrer le message suivant:

'PRZRFFNTRARPBAGVRAGEVRAQVAGRERFFNAGZNVFVYRFGFHSSVFNZRAGYBATCBHEDHRPRFBVGCRAVOYRQRYRQRPUVSSERENYNZNVA'

Exercice 2: masque jetable ou chiffre de Vernam

ÉnoncéCorrection

Dans le DL 0001, on a vu le principe du chiffre de Vernam, plus communément appelé masque jetable.

On y avait établi les fonctions:

def xor(a:str, b:str) -> str:
    '''
    revoie le résultat d'un XOR (ou exclusif) entre les caractères
    a et b, après conversion en code Unicode
    '''
    return chr(ord(a) ^ ord(b))

def masque_jetable(chaine:str, cle:str) -> str:
    '''
    Chiffre la chaine de caractère chaine selon le chiffre de
    Vernam avec la clé cle.
    '''
    texte_chiffre = ''
    for k in range(len(chaine)):
        texte_chiffre += xor(chaine[k], cle[k%len(cle)])
    return texte_chiffre

Déchiffrer le message : "\x0c!(8<en\x12%/=i\x1a&;'=.n ,<2 :s/'6;n7,n%&; h" sachant que la clé comporte trois lettres majuscules et que c'est moi qui l'ai choisie...

Dans le cas du masque jetable, si la clé (le masque) est aussi longue que le texte clair, alors il est impossible de retrouver le texte initial! En revanche, il faut impérativement changer le masque à chaque utilisation (d'où le terme jetable).

Avantage et inconvénient d'un chiffrement symétrique

Avantage: Les chiffrements symétriques sont souvent rapides, consommant peu de ressources et donc adaptés au chiffrement de flux important d'informations.

Comme nous le verrons, la sécurisation des données transitant par le protocole https est basée sur un chiffrement symétrique.
Inconvénient: La clé ! Si deux personnes (Alice et Bob dans la suite du cours) ont besoin d'utiliser un chiffrement pour se parler, comment peuvent-ils échanger leurs clés puisque leur canal de transmission n'est pas sûr ?

Le chiffrement symétrique impose qu'Alice et Bob aient pu se rencontrer physiquement au préalable pour convenir d'une clé secrète, ou bien qu'ils aient réussi à établir une connexion sécurisée pour s'échanger cette clé.

Quels sont les chiffrements symétriques modernes ?⚓︎

L'algorithme de chiffrement symétrique le plus utilisé actuellement est le chiffrement AES, pour Advanced Encryption Standard.

chiffrement par bloc de 128 bits, répartis dans une matrice de 16 octets (matrice carrée de taille 4).
ces 128 bits sont transformés par des rotations, multiplications, transpositions, [...] de la matrice initiale, en faisant intervenir dans ces transformations une clé de 128, 192 ou 256 bits.
pour l'AES-256 (avec une clé de 256 bits), l'attaque par force brute nécessiterait \(2^{256}\) opérations, soit un nombre à 78 chiffres...
il n'existe pas d'attaque connue efficace à ce jour. Les seules attaques sont des attaques sur des faiblesses d'implémentation, ou par canal auxiliaire.

2. Chiffrement asymétrique⚓︎

Bien que certains chiffrements symétriques sont efficaces, ils sont vulnérables si la clé est connue puisqu'elle sert également à déchiffrer. Parfois la clé de déchiffrement n'est pas exactement la même (comme dans le chiffre de César, où si \(n\) est la clé pour chiffrer alors on déchiffre avec \(-n\) ou \(26-n\)) mais elle se déduit de façon très simple de la clé de chiffrement.

Pour résoudre le problème de l'échange des clés, Whitfield Diffie et Martin Hellman (chercheurs à Stanford) proposent en 1976 un protocole qui repose en partie sur une information connue de tous et en partie sur une information gardée secrète par Alice et Bob...

Photo de Whitfield Diffie (à droite), Martin Hellman (au centre) et Ralph Merkle (à gauche) prise en 1977
Crédit: Stanford News Service

2.1 Échange de clés de Diffie-Hellman⚓︎

Principe

L'analogie la plus courante pour illustrer le protocole d'échange de clés de Diffie-Hellman est celui des pots de peinture: il est facile de mélanger deux peintures de couleurs différentes mais le contraire est impossible.

Étape 1Étape 2Étape 3Étape 4

Alice et Bob s'entendent sur une couleur (le jaune) et se la partagent publiquement.

Alice et Bob choisissent secrètement chacun une couleur: le magenta pour Alice et le cyan pour Bob, puis ils mélangent leur couleur avec la couleur commune.

Ils s'échangent publiquement les couleurs obtenues (orange et bleu). Même si Ève intercepte ces couleurs, elle ne peut pas les séparer!

Alice mélange sa couleur secrète (magenta) avec le mélange de Bob, et Bob fait de même avec la sienne et le mélange d'Alice. Au final, ils obtiennent le même mélange: c'est la clé !

En pratique, on n'utilise pas des pots de peinture (ça ne passe pas par la fibre ou la wifi) mais des fonctions mathématiques et des nombres entiers (très grands). L'idée de Diffie-Hellman est d'utiliser des fonctions de la forme \(x \rightarrow k^x \ (\text{mod}\ p)\) et utilisent les propriétés de l'arithmétique modulaire.

Arithmétique modulaire

Faire des calculs modulo un entier \(n\), c'est ne garder que le reste de la division euclidienne par \(n\).

Le fait que 15 soit égal à 1 modulo 7 (car \(15=2 \times 7+1\)) s'écrira \(15 \equiv 1 \ (\text{mod}\ 7)\).

De même, \(10 \equiv 3 \ (\text{mod}\ 7)\), \(25 \equiv 4 \ (\text{mod}\ 7)\), \(32 \equiv 2 \ (\text{mod}\ 10)\), etc.

En effet, s'il est assez simple de calculer une puissance «modulo p», il est en revanche compliqué de faire l'inverse (prendre le logarithme discret) car on ne connaît pas d'algorithme efficace pour certaines grandes valeurs de p. Cette arithmétique fournit donc d'assez bonnes fonctions «à sens unique» (fonction à trappe).

Exercice 3

ÉnoncéCorrection

Alice et Bob choisissent d'utiliser la fonction \(f(x) = 7^x \ (\text{mod}\ 11)\). C'est le jaune.

Alice choisit un nombre \(A=3\) et le garde secret (c'est le magenta). Elle calcule \(\alpha = f(A)\) (le orange) et l'envoie à Bob. Que reçoit Bob?
Bob choisit un nombre \(B=6\) et le garde secret (c'est le cyan). Il calcule \(\beta = f(B)\) (le bleu) et l'envoie à Alice. Que reçoit Alice?
Alice reçoit \(\beta\) de Bob et calcule \(\beta^A \ (\text{mod}\ 11)\). Bob reçoit \(\alpha\) d'Alice et calcule \(\alpha^B \ (\text{mod}\ 11)\). Quelle est la clé échangée?

Deux inconvénients majeurs résident cependant dans ce protocole:

il nécessite plusieurs échanges entre Alice et Bob;
il faut qu'ils soient tous les deux disponibles pour faire ces échanges, ce qui peut empêcher un chiffrement immédiat.

2.2 Cryptographie à clé publique⚓︎

Pour pallier à ces inconvénients, Diffie et Hellman imaginent un chiffrement où les clés servant à chiffrer et déchiffrer un message sont différentes: on parle alors de chiffrement asymétrique ou bien de chiffrement à clé publique. De plus ces clés ne doivent pas se déduire facilement l'une de l'autre: il faut utiliser une sorte de fonction à sens unique, qui soit simple à utiliser pour chiffrer, mais très difficile à inverser pour déchiffrer.

Le principe de base est l'existence d'une clé publique, appelée à être distribuée largement, et d'une clé privée, qui ne quitte jamais son propriétaire.

Principe

Étape 1Étape 2Étape 3

Alice fabrique une clé publique (le cadenas) et une clé privée (la clé du cadenas). Elle diffuse la clé à Bob (en réalité, à tout le monde, d'où le terme clé publique).

À l'aide de la clé publique d'Alice, Bob peut chiffrer son message et l'envoyer à Alice. Une fois son message chiffré, Bob lui-même ne peut pas revenir en arrière et déchiffrer son propre message puisqu'il ne connaît pas la clé privée d'Alice.

Grâce à sa clé privée, Alice peut déchiffrer et ouvrir le message qui lui est adressé.

Pourquoi ça marche?

Les clés sont des fonctions mathématiques (ou même simplement des nombres très grands): une fonction \(P\) qui permet de chiffrer les messages et sa fonction inverse \(S\) qui permet de déchiffrer, c'est-à-dire que \(S(P(\text{message})) = \text{message}\).

On peut fabriquer simultanément un couple \((P,S)\), mais connaissant uniquement \(P\), il est impossible (ou au moins très difficile) de retrouver \(S\). Et réciproquement.

La connaissance de \(P\) par un tiers ne compromet donc pas la sécurité de l'envoi des messages codés, puisqu'elle ne permet pas de retrouver \(S\). Il est possible de donner librement \(P\), qui mérite bien son nom de clé publique.

Enfin, il faut comprendre que ces clés ont un rôle interchangeable: on peut très bien chiffrer avec la clé privée et déchiffrer avec la clé publique (on verra plus loin dans le cours une utilisation de cette inversion).

2.3 Authentification: le double cadenas⚓︎

Dans la situation du 2.2, Alice (qui a distribué largement sa clé publique) ne peut pas s'assurer que le message vient bien de Bob. Il peut avoir été créé par Ève, qui signe «Bob» et usurpe ainsi son identité.

Le protocole - appelé signature électronique - que nous allons décrire ci-dessous permet :

d'empêcher qu'un message intercepté soit déchiffré (ce qui était déjà le cas dans le 2.1)
mais aussi de s'assurer que chaque personne est bien celle qu'elle prétend être : on résout le problème d'authentification.

Principe

Alice possède le couple clé publique/clé privée \((P_A, S_A)\) et Bob le couple \((P_B, S_B)\). Alice veut envoyer à Bob le message M.

Phase d'envoi: Alice chiffre M avec sa clé privée \(S_A\), c'est-à-dire qu'elle calcule \(M'=S_A(M)\). Puis elle chiffre \(M'\) avec la clé publique de Bob: elle envoie à Bob \(M''=P_B(M') = P_B(S_A(M))\).
Phase de réception: À l'aide de sa clé privée \(S_B\), Bob déchiffre \(M''\), c'est-à-dire qu'il calcule \(S_B(M'') =S_B(P_B(M')) = M'\). Seul lui peut effectuer ce calcul, d'où la sécurité de l'envoi, Ève ne peut rien faire du message \(M''\) envoyé par Alice.

Il calcule ensuite \(P_A(M')=P_A(S_A(M))=M\). Il est alors sûr que c'est Alice qui lui a envoyé ce message, car elle seule a pu calculer \(S_A(M)\).

En résumé :

Alice est sûre que seul Bob pourra déchiffrer le message qu'elle envoie.
Bob est sûr que le message qu'il reçoit vient bien d'Alice.

Ce protocole, s'il est fiable, est lent puisque deux fois plus lent qu'un algorithme à clé publique (lui-même déjà très lent!). En outre, il ne garantit pas l'intégrité du message, c'est-à-dire que celui-ci n'est pas altéré par des erreurs de transmission. L'utilisation des fonctions de hachage résout ces problèmes.

Supposons qu'Alice et Bob disposent d'une fonction de hachage \(h\) (SHA-256 par exemple):

Phase d'envoi: Alice calcule \(h(M)\) - le condensé - et envoie à Bob \(P_B(M)\) (calculé à l'aide de la clé publique de Bob) accompagné de \(S_A(h(M))\).
Phase de réception: Bob calcule \(S_B(P_B(M))=M'\). Puis il calcule \(P_A(S_A(h(M)))\), qu'il compare à \(h(M')\). Si les quantités sont égales, il est sûr que c'est bien Alice qui a envoyé le message, et que celui-ci a été correctement transmis.

3. Chiffrement RSA⚓︎

Lorsqu'en 1976 Diffie et Hellman présentent le concept de chiffrement asymétrique, ils en proposent uniquement un modèle théorique, n'ayant pas trouvé une réelle implémentation de leur protocole.

Trois chercheurs du MIT (Boston), Ron Rivest, Adi Shamir et Len Adleman se penchent alors sur ce protocole, convaincus qu'il est en effet impossible d'en trouver une implémentation pratique. En 1977, au cours de leurs recherches, ils démontrent en fait l'inverse de ce qu'ils cherchaient : ils créent le premier protocole concret de chiffrement asymétrique : le chiffrement RSA.

De gauche à droite: Adi Shamir, Ron Rivest, Len Adleman

Au même moment à Londres, Clifford Cocks, (chercheur au très secret GCHQ) apprend que Rivest Shamir et Adleman viennent de découvrir ce que lui-même a découvert 3 ans auparavant mais qui est resté classé Secret Défense.

Il est le véritable inventeur du RSA... mais le reste du monde ne l'apprendra qu'en 1997 au moment de la déclassification de cette information.

Principe

Le chiffrement RSA est basé sur l'arithmétique modulaire.

Étape 1Étape 2Étape 3Étape 4Étape 5Étape 6

Alice choisit 2 grands nombres premiers \(p\) et \(q\). Dans la réalité ces nombres seront vraiment très grands (plus de 100 chiffres). Dans notre exemple, nous prendrons \(p = 3\) et \(q = 11\).

Alice multiplie ces deux nombres \(p\) et \(q\) et obtient ainsi un nombre \(n\).

Il est très facile pour Alice de calculer \(n\) en connaissant \(p\) et \(q\), mais il extrêmement difficile pour Ève de faire le travail inverse car trouver \(p\) et \(q\) en connaissant \(n\) prend un temps exponentiel avec la taille de \(n\).
C'est sur cette difficulté (appelée difficulté de factorisation) que repose la robustesse du système RSA.

Alice choisit un nombre \(e\) qui doit être premier avec \((p-1)(q-1)\). On note \(\phi(n)\) le nombre \((p-1)(q-1)\).

Dans notre exemple, \((p-1)(q-1) = 20\), Alice choisit donc \(e = 3\). (mais elle aurait pu aussi choisir 7, 9, 13...).

Le couple \((e, n)\) sera la clé publique d'Alice. Elle la diffuse à qui veut lui écrire.

Dans notre exemple, la clé publique d'Alice est \((3, 33)\).

Alice calcule maintenant sa clé privée : elle doit trouver un nombre d qui vérifie l'égalité \(e \times d \equiv 1 \ (\text{mod}\ \phi(n))\).

Dans notre exemple, comme \(7 \times 3 \equiv 1 \ (\text{mod}\ 20)\), ce nombre \(d\) est égal à 7.

En pratique, il existe un algorithme simple (algorithme d'Euclide étendu) pour trouver cette valeur \(d\), appelée inverse de e modulo \(\phi(n)\).

Le couple \((d, n)\) sera la clé privée d'Alice. Elle ne la diffuse à personne.

Dans notre exemple, la clé privée d'Alice est \((7, 33)\).

Supposons que Bob veuille écrire à Alice pour lui envoyer le nombre 4. Il possède la clé publique d'Alice, qui est \((3, 33)\).

Il calcule donc \(4^3\) modulo 33, qui vaut 31. C'est cette valeur 31 qu'il transmet à Alice.

\[4^3 \equiv 31 \ (\text{mod}\ 33)\]

Si Ève intercepte cette valeur 31, même en connaissant la clé publique d'Alice (3,33), elle ne peut pas résoudre l'équation \(x^3 \equiv 31 \ (\text{mod}\ 33)\) de manière efficace.

Alice reçoit la valeur 31.
Il lui suffit alors d'élever 31 à la puissance 7 (sa clé privée), et de calculer le reste modulo 33 :

\(31^7 = 27512614111\)

\(27512614111 \equiv 4 \ (\text{mod}\ 33)\)

Elle récupère la valeur 4, qui est bien le message original de Bob.

Comment ça marche ?

Grâce au Petit Théorème de Fermat, on démontre (voir ici) assez facilement que \(M^{ed} \equiv M [n]\). Il faut remarquer que \(M^{ed} = M^{de}\). On voit que les rôles de la clé publique et de la clé privée sont symétriques : un message chiffré avec la clé publique se déchiffrera en le chiffrant avec la clé privée, tout comme un message chiffré avec la clé privée se déchiffrera en le chiffrant avec la clé publique.

Animation interactive voir https://animations.interstices.info/interstices-rsa/rsa.html

RSA, un système inviolable ?⚓︎

Le chiffrement RSA a des défauts (notamment une grande consommation des ressources, due à la manipulation de très grands nombres). C'est pourquoi on l'utilise plutôt pour sécuriser l'échange d'une clé d'un chiffrement symétrique (comme AES par exemple). Mais le choix d'une clé publique de grande taille (actuellement 1024 ou 2048 bits) le rend pour l'instant inviolable.

Actuellement, il n'existe pas d'algorithme efficace pour factoriser un nombre ayant plusieurs centaines de chiffres.

Deux évènements pourraient faire s'écrouler la sécurité du RSA :

la découverte d'un algorithme efficace de factorisation, capable de tourner sur les ordinateurs actuels. Cette annonce est régulièrement faite, et tout aussi régulièrement contredite par la communauté scientifique. (voir, le 05/03/2021, https://www.schneier.com/blog/archives/2021/03/no-rsa-is-not-broken.html)
l'avènement d'ordinateurs quantiques, dont la vitesse d'exécution permettrait une factorisation rapide. Il est à noter que l'algorithme de factorisation destiné à tourner sur un ordinateur quantique existe déjà : l'algorithme de Schor.

4. HTTPS⚓︎

Aujourd'hui, plus de 90 % du trafic sur internet est chiffré : les données ne transitent plus en clair (protocole http) mais de manière chiffrée (protocole https), ce qui empêche la lecture de paquets éventuellements interceptés.

Ce protocole n'utilise pas le chiffrement asymétrique (RSA par exemple), car il est très gourmand en ressources. Le chiffrement/déchiffrement doit être rapide pour ne pas ralentir les communications ou l'exploitation des données par les utilisateurs!

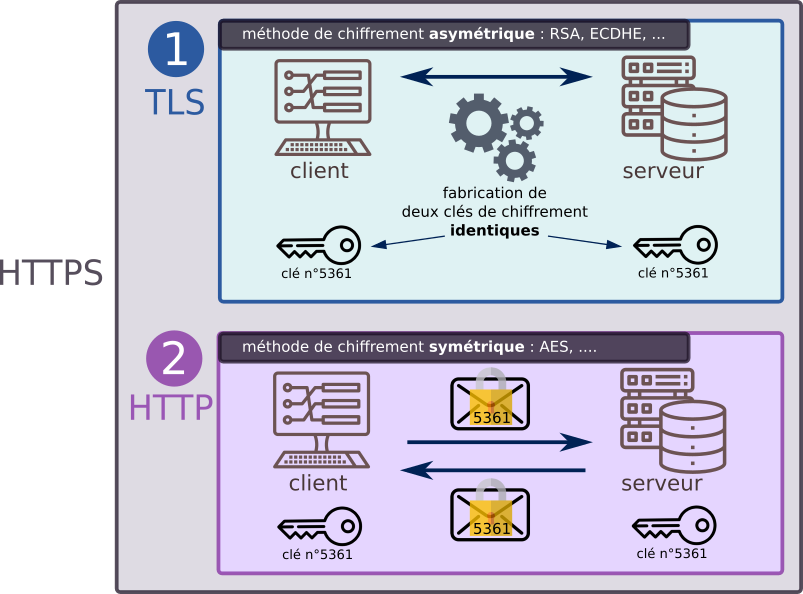
HTTPS est donc un exemple d'utilisation conjointe d'un chiffrement asymétrique et d'un chiffrement symétrique:

Le chiffrement asymétrique est réservé à l'échange de clés (au début de la communication).
Le chiffrement symétrique, bien plus rapide, prend ensuite le relais pour l'ensemble de la communication.

Principe

Le protocole https est la réunion de deux protocoles :

le protocole TLS (Transport Layer Security, qui a succédé au SSL) : ce protocole, basé sur du chiffrement asymétrique, va conduire à la génération d'une clé identique chez le client et chez le serveur.
le (bon vieux) protocole http, mais qui convoiera maintenant des données chiffrées avec la clé générée à l'étape précédente. Les données peuvent toujours être interceptées, mais sont illisibles. Le chiffrement symétrique utilisé est actuellement le chiffrement AES.

Fonctionnement du TLS : explication du handshake (Hors programme)⚓︎

Observons en détail le fonctionnement du protocole TLS, dont le rôle est de générer de manière sécurisée une clé dont disposeront à la fois le client et le serveur, leur permettant ainsi d'appliquer un chiffrement symétrique à leurs échanges.

étape 1 : le «client Hello». Le client envoie sa version de TLS utilisée.
étape 2 : le «server Hello». Le serveur répond en renvoyant son certificat prouvant son identité, ainsi que sa clé publique.
étape 3 : le client interroge l'autorité de certification pour valider le fait que le certificat est bien valide et que le serveur est bien celui qu'il prétend être. Cette vérification est faite grâce à un mécanisme de chiffrement asymétrique.

La présentation du certificat à l'autorité de certification peut se représenter comme le scan d'une pièce d'identité dans un aéroport. L'autorité de certification est alors l'État (dont la base de données est interrogée par un logiciel) qui valide que la pièce d'identité est bien un document officiel.

étape 4 : une fois vérifiée l'authenticité du serveur et que son certificat est valide, le client calcule ce qui sera la future clé de chiffrement symétrique (appelée «clé AES» dans l'infographie). Cette clé est chiffrée avec la clé publique du server (transmise à l'étape 1), ce qui assure la sécurité de son transfert. Le serveur déchiffre cette clé grâce à sa clé privée, et dispose ainsi lui aussi de la clé.

Le transmission par protocole http de données chiffrées au préalable avec la clé AES peut commencer.

Remarque : en réalité, ce n'est pas la clé AES qui est transmise à l'étape 4, mais un nombre choisi par le client, qui permettra, avec deux autres nombres choisis par le client (étape 1) et le serveur (étape 2) de reconstituer la clé AES, qui sera donc identique côté client et côté serveur.

À propos du certificat

Sur Firefox par exemple, en cliquant sur l'icone cadenas à gauche de la barre d'adresse, on peut récupérer le certificat (en général un fichier binaire au format X.509) du site au format PEM. À l'aide ensuite d'OpenSSL par exemple, on peut consulter le contenu du fichier avec:

openssl x509 -in github-io-chain.pem -text

Certificate:
Data:
    Version: 3 (0x2)
    Serial Number:
        04:4d:72:d7:7c:dd:a7:02:dd:5a:67:f2:a2:3b:bd:d9
    Signature Algorithm: sha256WithRSAEncryption
    Issuer: C = US, O = DigiCert Inc, CN = DigiCert TLS RSA SHA256 2020 CA1
    Validity
        Not Before: Feb 21 00:00:00 2023 GMT
        Not After : Mar 20 23:59:59 2024 GMT
    Subject: C = US, ST = California, L = San Francisco, O = "GitHub, Inc.", CN = *.github.io
    Subject Public Key Info:
        Public Key Algorithm: rsaEncryption
            Public-Key: (2048 bit)
            Modulus:
                00:b8:b0:60:0e:1a:2f:f1:b1:86:4b:64:ec:11:9f:
                [...]
                2c:2c:ec:f8:39:09:36:bd:19:8d:03:56:41:66:07:
                24:e3
            Exponent: 65537 (0x10001)
[...]
Signature Algorithm: sha256WithRSAEncryption
Signature Value:
    37:a4:1b:11:22:9f:fc:9f:c9:67:07:8f:aa:86:13:9f:e0:08:
    1d:6e:0c:8d:65:fb:03:79:50:c6:76:ba:30:90:a0:a4:1c:79:
    13:07:b9:5a:18:8d:97:4c:05:71:8a:d0:22:17:c6:19:a2:22:
    8b:03:f6:2c:84:71:6c:55:df:e2:99:43:65:e5:d7:b7:b7:37:
    4c:c6:c8:e5:f1:d8:a7:7b:07:5d:eb:b8:1c:50:a4:a3:8e:f0:
    4c:f8:b8:6a:72:59:be:43:0e:8a:de:b5:5e:8f:9e:3f:5a:43:
    64:82:cc:e0:de:76:f4:be:a6:12:0a:06:68:bb:77:e1:4c:ef:
    4b:4d:67:af:f6:72:c7:6b:1b:9c:48:53:a7:7f:ed:76:18:5c:
    f0:f6:c6:4c:24:53:57:57:e1:42:a6:3d:ae:e1:f5:93:f2:6a:
    fa:29:72:01:3e:b7:06:f1:2f:1a:0e:91:c5:ec:35:bf:f5:da:
    33:95:de:24:12:0d:f5:c3:23:8d:40:82:d1:5c:eb:de:0a:08:
    e8:e5:83:e5:0a:8b:3a:5e:98:4e:77:4f:9f:dc:ab:7e:ce:a8:
    28:4f:aa:79:4f:c9:be:8f:60:88:6e:6b:f9:20:6c:7f:38:96:
    d6:da:d7:11:03:43:d8:b8:51:87:ce:32:22:4d:64:4c:c4:75:
    27:d0:e3:df

5. Exercices⚓︎

Exercice 4: Chiffrement affine

ÉnoncéCorrection

Principe

Chaque lettre est codée par son rang dans l'alphabet: A → 0, B → 1, etc.
On applique à chaque rang la transformation affine \(f(x)=(ax+b)\%26\) où \(a\) et \(26\) sont deux nombres entiers, premiers entres eux (c'est-à-dire n'admettant pas de diviseur commun autre que 1).

Écrire une fonction affine.
Décoder la phrase UCGXLODCMOXPMFMSRJCFQOGTCRSUSXC, sachant qu'elle contient le mot TRAVAIL et que \(a\) et \(b\) sont inférieurs à 20.

# 1.
def affine(msg:str, a:int, b:int) -> str:
    '''
    Renvoie le texte msg chiffré avec la méthode du chiffrement affine avec a, b comme clé.
    '''
    msg_chiffre = ''
    for caractere in msg:
        rang = ord(caractere) - 65
        rang_chiffre = (a*rang + b) % 26
        caractere_chiffre = chr(rang_chiffre + 65)
        msg_chiffre += caractere_chiffre
    return msg_chiffre

# 2.
def trouve_cle(msg:str, mot:str) -> tuple:
    '''
    Renvoie la clé a, b si le mot chiffré est dans le message msg.
    '''
    for a in range(1, 21):
        for b in range(21):
            mot_chiffre = affine(mot, a, b)
            if mot_chiffre in msg:
                return a, b

def dico_dechiffrement(a:int, b:int):
    '''
    Construit un dictionnaire de déchiffrement dont les clés sont les lettres
    chiffrées et les valeurs les lettres claires.
    '''
    dico = {}
    for k in range(26):
        caractere = chr(65 + k)
        dico[affine(caractere, a, b)] = caractere
    return dico

def dechiffre_affine(msg:str, mot:str) -> str:
    '''
    Déchiffre un message chiffré msg connaissant un mot du texte clair.
    '''
    a, b = trouve_cle(msg, mot)
    msg_clair = ''
    d = dico_dechiffrement(a, b)
    for caractere in msg:
        msg_clair += d[caractere]
    return msg_clair

Exercice 5: RSA 1

ÉnoncéCorrection

Le module pycryptodome contient tout un tas d'outils cryptographiques, dont ceux nécessaires pour travailler sur RSA. Dans un terminal, installez le avec la commande:

sudo pip3 install pycryptodome

Code à compléter
import Crypto
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Random import get_random_bytes 

# Un peu d'arithmétique modulaire
def euclide_etendu(a:int, b:int) -> int:
    '''
    Renvoie un tuple (u, v) d'entiers tels que a*u + b*v = pgcd(a, b)
    '''
    r, u, v, rp, up, vp = a, 1, 0, b, 0, 1
    while rp != 0:
        q = r // rp
        r, u, v, rp, up, vp = rp, up, vp, r - q*rp, u - q*up, v - q*vp
    return u, v

def inverse(a:int, m:int) -> int:
    '''
    Renvoie l'inverse u de a modulo m, c-a-d tel que a*u = 1 (mod m).
    '''
    u, v = euclide_etendu(a, m)
    if u < 0:
        return u + m
    return u

# 
bits = 512
msg = "en NSI on fait de la crypto"

p = Crypto.Util.number.getPrime(bits, randfunc=get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=get_random_bytes)

n = ...
phi = ...

e = 65537  # 65537 est un nombre premier, donc forcément premier avec phi
d = ...

M = bytes_to_long(msg.encode('utf-8'))

M_chiffre = pow(M, e, n) # M puissance e modulo n
M_dechiffre = pow(...)

print(long_to_bytes(M_dechiffre))

Compléter le code ci-dessus, puis l'exécuter. Examiner le contenu des différentes variables.
En adaptant le code précédent, déchiffrer le message suivant, sachant que \(p\) et \(q\) sont les 13ème et 14ème nombres premiers de Mersenne. 3321201356966590346561115071776627133387292843371714010408399835551061020050045365398836013027686993987632768071673564690778259745221441566760245236779498669656980590070600792357065491110399368931370008478330254358972461518602964119545062624451642219086661534670622352070903070456403667523575064863364819845990986678472406418837664850717889

Exercice 6: RSA 2

ÉnoncéCorrection

En règle générale, les clés publiques sont échangées en PEM qui est une version texte encodée en Base64 comme par exemple:

À propos de la Base64

import base64

msg = "en NSI on fait de la crypto"
msg_bytes = msg.encode('utf-8')
print(msg_bytes)
msg_b64 = base64.b64encode(msg_bytes)
print(msg_b64)
msg_b64_decode = base64.b64decode(msg_b64)
print(msg_b64_decode)
print(msg_b64_decode.decode('utf-8'))

On peut l'obtenir par exemple ainsi:

from Crypto.PublicKey import RSA

cle_privee = Crypto.PublicKey.RSA.construct((n, e, d))
cle_publique = cle_privee.publickey()
print(cle_publique.exportKey().decode())

On peut également récupérer très facilement l'exposant (e) et le module (n) connaissant la clé publique:

from Crypto.PublicKey import RSA

cle_publique = RSA.importKey("""\
-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAzPtKIAxSBQXAyDp+uH3p
wroOSTVSPr/K1I7MQYqXhd2bZ1Y1ZosYsRaKyKIRScoez4yoI0+9Li4yMh692tHV
phInz0+FmocAqsQlUeozsdRt0mUJi20ujjwkRozesZY5J5RB+54oxX5uk9XRAFmf
HdNqZO3lNvM5QZC9CjowDJu/Cs7khHoUPDX1SeKKYd7iv70DYwDG/NYtBf+gaxY6
gaFdTmduFMN3wOnxnaRrl5f8tyNTHMHpRWPti1Q/N+CNIbM7NySb3IJMMKj+hj/N
xhk+lGizdIG469OZqICuDkSLBwxxaj9gb26uVv4/W7HLv9oXR1wwAB210rKSoQBz
5wIDAQAB
-----END PUBLIC KEY-----""")

print(cle_publique.e, cle_publique.n)

Récupérer les exposants et les modules des deux clés publiques données . Que remarque-t-on?

Une faille de RSA consiste justement à conserver le même module en changeant uniquement les exposants, ce qui pourrait pourtant être pratique plutôt que de créer un nouveau module de chiffrement à chaque utilisation de RSA.

C'est le point de départ de l'attaque des modules communs, qui nécessite d'obtenir le même message chiffré avec deux clés publiques \((e_1, n)\) et \((e_2, n)\).

Les voici:

message1 = 'A4ZTqgJUEUp3mJoaoNEkempFbBtUoDtX0Ak8sZembkpdR2FlgftR20u+ymLKGydBH9sV10vHhFEVGsaEfigaEZGC9wu7eo0irPY2J7khDP3QOA7qg3WJmvefne5VxeMU/gh65irNjp6O1jiXtdqTvMypqzHDIKuw68XIEF2J/aCw5nhIwCbBgQdIy7PYdxytoCbA4A0mJkdh4B2fVAoym0M+vDM7IP9ep371TLP/kPhcyrrv0FmGZCz3xM2Q+zsKrlqLkEb736KREg6JTpNjwfzaKHrTe/XP2sailo1x2IQIxltuR5Lv/9vFq7TP5qYG5aAfW0ReiLGhXTIXWBrgjQ=='

message2 = 'IJmhgMZG5YscMcnlmyQkrWb2P1WLDRx1JxxCTcK4OVJVetAtPIX5DvNGBhaWh7Rp9EXPq0k4YP/DI+k4Hq5i+2/RxUIaKXRYkBbOFx5WMloyn9wU0unRktdFX1Lv+Lg+uXA6oYFTQQkjc/lBWS9MEPRzzenPU+y/zghNs7k7lYj93e51jdQAz/LNz08KOqh0lalPtqjsrmDZ/6HVqESz7y4EkdZmk1iU9eg0E2/OWx0n5eC/jytemtIVrsOHfMXjmcY/MmZP93i1MTX1QzkFZrRe/55VgY6/fOLDYY7kTF1E8w+f16lfJFo31Ir+a6y9vjMZCBj3AkaW2DKCVFeLHw=='

Principe (mathématique) de l'attaque

Puisque les deux exposants \(e_1\) et \(e_2\) sont des nombres premiers (c'est le cas en général en pratique, le vérifier ici...), ils sont premiers entre eux donc le théorème de Bezout assure l'existence de deux entiers \(u\) et \(v\) tels que \(e_1\times u + e_2\times v =1\).

Or si on note \(C_1\) et \(C_2\) les deux messages chiffrés et \(M\) le message clair, on a \(C_1 = M^{e_1} (\text{mod } n)\) et \(C_2 = M^{e_2} (\text{mod } n)\).

Donc un «simple» calcul montre que \(C_1^u \times C_2^v = (M^{e_1})^u \times (M^{e_2})^v = M^{e_1 \times u + e_2 \times v} = M (\text{mod } n)\) !

En revanche, il reste un point un peu compliqué: en réalité \(v\) est négatif... Pour calculer \(C_2^v\), il faut en fait calculer son inverse modulo \(n\) puis élever celui-ci à la puissance \(-v\).

Vous disposez donc:

de la fonction euclide_etendu qui fournit les coefficients \(u\) et \(v\);
de la fonction inverse;
de la fonction base64.b64decode qui convertit de la Base64 en bytes (octets);
des fonctions bytes_to_long et long_to_bytes qui font les conversions octets ⟷ entiers.

Décodez donc le message échangé...